Equilibrio Traslacional

   INTRODUCCIÓN

Esta condición de equilibrio implica que una fuerza aislada aplicada sobre un cuerpo no puede producir por sí sola equilibrio y que, en un cuerpo en equilibrio, cada fuerza es igual y opuesta a la resultante de todas las demás. Así, dos fuerzas iguales y opuestas, actuando sobre la misma línea de acción, sí producen equilibrio.

El equilibrio puede ser de tres clases: estable, inestable e indiferente. Si un cuerpo está suspendido, el equilibrio será estable si el centro de gravedad está por debajo del punto de suspensión; inestable si está por encima, e indiferente si coinciden ambos puntos. Si un cuerpo está apoyado, el equilibrio será estable cuando la vertical que pasa por el centro de gravedad caiga dentro de su base de sustentación; inestable cuando pase por el límite de dicha base, e indiferente cuando la base de sustentación sea tal que la vertical del centro de gravedad pase siempre por ella.

                                          

                                                                       

CONTENIDO 

seguramente estas familiarizado con la idea básica del concepto fuerza. De tu experiencia cotidiana sabes que aplicas una fuerza cuando jalas o empujas algún objeto. Cuando pateas un balón sabes que aplicas una fuerza. Tal vez creas que la fuerza se asocia con el movimiento, sin embargo, no siempre que se aplica una fuerza se produce movimiento. Si empujas una de las paredes de tu salón de clases verás que no se produce movimiento alguno a pesar del esfuerzo que haces.

Decimos que un objeto se encuentra en equilibrio si no esta acelerado. Por tanto el equilibrio considera dos situaciones: cuando el objeto esta reposo o bien cuando se mueve de una velocidad constante en una trayectoria rectilínea

Decimos que un objeto esta en equilibrio traslacional cuando se encuentra en reposo o bien se mueve en línea recta con velocidad constante.

Equlibrio Traslacional

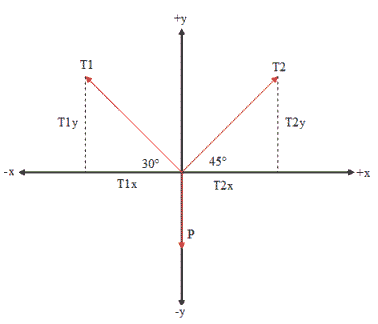
Se toma en cuenta la fuerza que actua sobre un cuerpo estas fuerzas se descomponen en dos componentes vectoriales VX y VY para calcular su valor matematico se tiene que saber el valor numérico de dicha fuerza para calcular a su vez la tencion que ejerce sobre el cuerpo. Existen dos condiciones y las cuales son :

Tax = tbx

tay + tby = c

Tipos de fuerzas que utiliza el Equilibrio Traslacional:

Fuerza de Tensión:

La tension es la fuerza que va por la cuerda en contrario al cuerpo, por ejemplo: si esta colgando entonces  la tensión va hasia arriba, es como si estiras una cuerda de boongy,si la estiras mucho esta te atrae, AHÍ es la fuerza de tensión, ve que al centro de la cuerda. En este caso no hay fuerza normal, ya que solo se produce en cuerpos que estan sobre una superficie, si están en el aire colgados no hay fuerza normal.

Fuerza de Comprensión:

El esfuerzo de comprensión es la resultante de las tensiones o presiones que existen dentro de un sólido deformable o medio contínuo, caracterizada porque tiende a una reducción de volumen o acortamiento en determinada dirección y también, la fuerza de comprensión es la contraria a la de tracción, intenta comprimir un objeto en el sentido de la fuerza.

Pesos:

En Física, el peso de un cuerpo se define como un vector que tiene magnitud y direccion, que apunta aproximadamente hacia el centro de la tierra. el vector peso es la fuerza con la cual un cuerpo actúa sobre un punto de apoyo, a causa de la atracción de este cuerpo por la fuerza de la gravedad.

Un cuerpo se encuentra en equilibrio traslacional cuando la sumatoria de todas las componentes en X es igual a 0 y a todas las componentes en Y es igual a 0. Cuando un cuerpo esta en equilibrio traslacional no tiene fuerza resultante actuando sobre el.

EJERCICIOS DEL EQUILIBRIO TRASLACIONAL

EJERCICIO # 1

Tensión	X	Y
A	(cos 135) Ax	(sen135)Ay
B	(cos50)Bx	(sen50)By
C	o	-250

tax-tbx
(cos135) Ax=(cos50)Bx
      -0.70 Ax = 0.64Bx
               Ax=  0.64Bx
                        -0.70
               Ax= -0.91 Bx                                            - Los Tres lados ya estan resueltos
                                                                                                     debidamente.




Tay + Tby= C                                                          

(Sen 135°) Ay (Sen 50°) By= -250
0.70 Ay + 0.5 By= -250
(0.70) (0.5 + 0.91) By =-250
0.35 + 0.91 By= -250
      1.26= -250
       B= -250
              1.26
       B= -198.04 N
                                                                      A= -0.91 Bx
                                                                      A=  (-0.91) (-198.04 N)
                                                                      A= -188.02 N



                                                            EJERCICIO # 2

                                 

Tensión	X	Y
A	(Cos 120°) Ax	(Sen 120°) Ay
B	(Cos 0°) Bx	0
C	0	-200 N

Tax = Tbx
(Cos120°) Ax= (Cos0°) Bx
-0.50 Ax =1Bx
         Ax = 1Bx = -2Bx
                  -0.50
                                                                                - Los tres lados ya estan resueltos
                                                                                                  debidamente.
Tay + Tby = C
Sen 120° Ay = -200 N
(0.87) (-2By) = -200 N
-1.74 By = -200 N
         B = -200 N = 114.94 N
                  -1.74
                                                                    A= -2 Bx
                                                                    A= -2 (114.94 N)
                                                                    A= -229.88 N

                           
                                                                EJERCICIO # 3

Tensión	X	Y
A	(Cos 150°) A	(Sen 150°) A
B	(Cos 40°) B	(Sen 40) B
C = 100 N	0	-100 N

Tax = Tbx                                                                  Tay + Tby = C
(Cos 150°) A = (Cos 40°) B                                      (Sen 150°) Ay + (Sen 40°) By= -100 N
               -0.87 Ax = 0.77 Bx                                      0.50 Ay + 0.64 By = -100 N
                        Ax = 0.77 Bx                                      (0.50) (-0.89 By) + 0.64 By = 100 N
                                -0.87
                         A = -0.89 Bx

-0.45 By + 0.64 By = -100                          A= (-0.89) (-526.32 N)
 0.19 By = -100 N                                       A= 468.42 N
          B = -100 N                                              
                   0.19
           B = -526.32                                         -Los tres lados ya estan resueltos
                                                                                        debidamente.
                                               

                                           

        A continuacion les presentaremos un tutorial donde les explicaremos detalladamente mas y mas acerca de lo que es el Equilibrio Traslacional:

Conclusión Acerca del Equilibrio Traslacional.

en esta conclusion damos a entender que el equilibrio traslacional en la fisica aplicada es muy importante ya que nosotros lo ponemos en practica todos los dias tanto en las actividades laborales diarias y asi como tambien en las actividades profesionales que tambien diariamente hacemos. es muy importante aprender mucho acerca de este tema ya que aprendemos para poner en practica muchos aprendizajes en la vida diaria. es muy importante aprender muchos prospectos sobre la fisica aplicada.

Si he logrado ver mas lejos, ha sido porque he subido a hombros de gigantes.
Isaac Newton.